Circular Shifting – DFT Property Matlab Program

Circular Shifting

Circular shifting: as the name implies, the Discrete Fourier Transform (DFT) is purely discrete: discrete-time data sets are converted into a discrete-frequency representation. This is in contrast to the DTFT that uses discrete time but converts to continuous frequency. Since the resulting frequency information is discrete in nature, it is very common for computers to use DFT calculations when frequency information is needed.

Using a series of mathematical tricks and generalizations, there is an algorithm for computing the DFT that is very fast on modern computers. This algorithm is known as the Fast Fourier Transform (FFT), and produces the same results as the normal DFT, in a fraction of the computational time as ordinary DFT calculations.

Let’s discuss circular shifting

Circular Time Shifting is very similar to regular, linear time shifting, except that as the items are shifted past a certain point, they are looped around to the other end of the sequence. This subject may seem like a bit of a tangent,

Here is the program for the DFT property

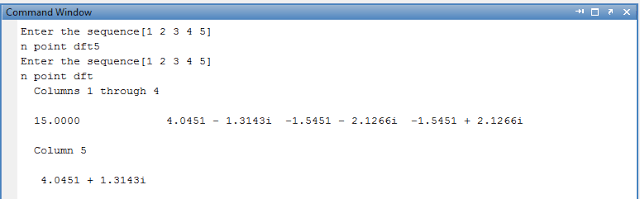
x = input('Enter the sequence');
N = input('n point dft');
z = fft(x,N);
l =2;
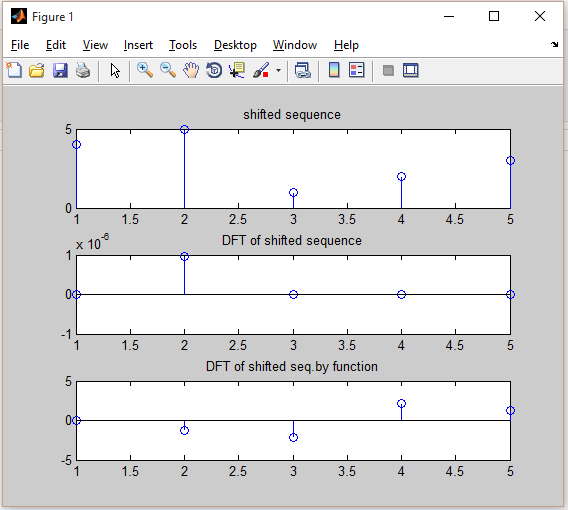
f = circshift(x,[1,l]);
subplot(3,1,1);
stem(f);
title('shifted sequence');
y =0;
for p =1:N
y(p) = 0;
k =p;
y(p) = (z(k)*exp(-i*2*pi*(k-1)*l/N));
end
subplot(3,1,2);
stem(y);
title('DFT of shifted sequence');
W = fft(f);
subplot(3,1,3);
stem(W);
title('DFT of shifted seq.by function');
disp (W)

 

[mks_separator style=”double” height=”2″]

You can ask all your Matlab related queries and doubts in comments below and we will be more than happy to answer all your questions